状況解説
今回解説するのは「双兵(2枚の兵)」対「単士象(守り駒は士1枚と象1枚)」という状況の残局です。
これに似た形の「双兵対双士」と「双兵対双象」については以前紹介し、勝ちと和のポイントについてそれぞれ解説しました。
今回はその時のことを思い出しながら、守り駒が単士象の場合はどんな結果になるのかを見ていきましょう。
例題①
まずは最も強い双高兵の場合から見ていきましょう。
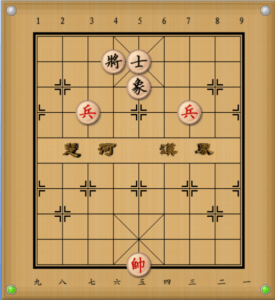
- 兵七進一 象5進3
- 兵七進一 将4退1
- 兵三進一 象3退5
- 兵三進一 士5進6
- 兵三平四 象5進3
- 帥五進一 象3退5(和)
まずは和という結果に驚かれた方が多いのではないでしょうか?
以前紹介した「双兵対双士」と「双兵対双象」のいずれも、双高兵の場合は必勝で簡単に勝つことができました。
しかし黒の守りが単士象の場合は、たとえ双高兵でも勝つことができないんです。
手順を少し具体的に見ていきましょう。
2回合兵七進一に対し将4進1は、兵三平四から兵を寄せていき紅の勝ち。
将を下段に落とすことに成功し、さらには右辺からも兵が迫って紅の攻めは調子が良さそうです。
しかし5回合兵三平四のあとの局面を考えてみると、意外にも攻めの後続手がないんです。
6回合で一応紅には兵四進一(次に兵四平五の殺)という手がありますが、士6退5と引かれたときやはり次がありません。
もちろんこの手順以外にも動かし方はたくさん考えられますが、どれも黒が正しく対処すれば結果は和になります。
今回の黒の守りである単士象は、守り駒の数は双士・双象の時と同じ2枚です。
しかし士の長所である九宮の守り、象の長所である広い移動範囲の両方を兼ね備えているため、双士・双象の時よりもはるかに防御力が高くなっています。
そのため自分が双兵で攻めるとき、双士・双象と単士象はきっちり区別して考えるようにしましょう。
例題②
次はこの局面を見ていきましょう。
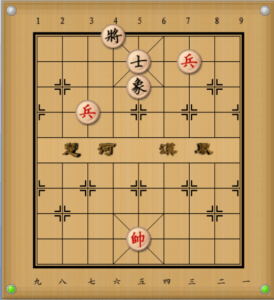
- 兵三平四
考えられる黒の受け方は4通り
手順①
- ・・・・ 将4進1
- 兵七平六 士5退4
- 帥五平六 士4進5
- 帥六退一 象5進7
- 帥六平五 士5退4(和)
*5回合黒が象7退5とした場合は、兵四平五、将4平5、兵六進一で紅勝ち。
手順②
- ・・・・ 士5退6
- 兵七平六 将4進1(それ以外は紅勝)
- 兵四進一 象5進7
- 帥五平六 将4平5(和)
手順③
- ・・・・ 将4平5
- 兵七平六 士5退6
- 兵六進一 将5平4
- 兵六平五 将4進1
- 兵四進一 (紅勝)
手順④
- ・・・・ 士5進6
- 兵七平六 将4進1
- 兵六平五 象5進3
- 兵五平四 将4進1
- 後兵進一 将4退1
- 前兵平五 将4進1
- 帥五退一 象3退1
- 兵四平五 (紅勝)
紅の初手兵三平四には4通りの受け方がありますが、皆さんはどれが和になってどれが紅勝ちかをしっかり判別できたでしょうか?
実際には手順①と手順②が和で、手順③と手順④が紅勝ちという結果になります。
この例題から分かるのは、「双兵対単士象」がいくら防御力が高く和になりやすい残局だと言っても、しっかりとした正確な読みがないと自分が守備側の時に和にするのは難しいということです。
そのため「双兵対単士象」になったからと言って安心することなく、しっかり最後まで読みを怠らず指すようにしましょう。
例題③
最後にこの局面を考えてみましょう。
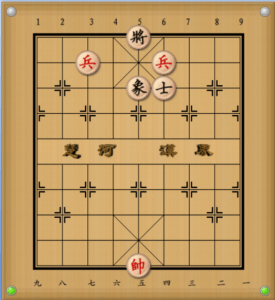
- 兵七平六 士6退5
- 兵四平五 将5平6
- 兵六進一 象5進3
- 兵六平五 (紅勝)
ここまで「双兵対単士象」は守備側の防御力が高いため和になりやすい残局だとお伝えしてきました。
ただどんな場合も和になる必和残局ではなく、もちろん紅が勝てる状況もあります。
例題③では初手で兵七平六とし、殺法の時に紹介した二鬼拍門の格好になりました。
これによって将は肋道に逃げ出すことができなくなり、以下簡単に紅勝ちとなります。
このように2枚の兵を二鬼拍門の位置に配置するのが、「双兵対単士象」で勝つときの代表的な形です。
ただこうなれば必ず勝ちという訳ではなく、帥の位置(どの線にいるか)や士相の有無も関わってくることがあるので、紅としても勝てるかどうかは慎重に考える必要があります。
例A:帥の位置(線)が悪いので和
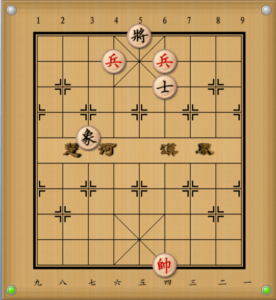
- 帥四進一 象3退1
- 帥四退一 象1進3(和)
例B:士があるため帥が左辺に移動でき紅勝。
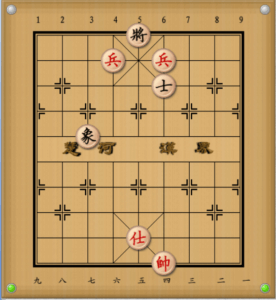
- 帥四平五 象3退1
- 帥五平六 士6退5(象1進3は兵六進一で紅勝)
- 兵六平五 (紅勝)
またもし例題③が黒の手番だった場合は、将5平4と肋道を先に抑え進路を確保すれば必和残局になります。
このあたり少しややこしいですが、しっかり整理して理解しておきましょう。
まとめ
「双兵対単士象」の残局は、
兵の位置を問わず全体的に和になりやすい。
ただ紅が勝てる局面もあり、士相の有無が結果に影響する場合もある。
という結論になります。

