状況解説
今回解説するのは「三兵(3枚の兵)」対「馬双士(守り駒は馬1枚と士2枚)」という状況の残局です。
以前紹介した「三兵対士象全」は高兵なら必勝の残局でしたが、今回は黒の象2枚が馬1枚に変わりました。
駒の価値としてはどちらも4ポイントでほとんど同じですが、残局の場合はどうなるのでしょうか?
早速見ていきましょう!
例題①
まずはこの局面です。
三高兵の形から兵が侵攻し、将をかなり追い詰めています。
紅はこの形から勝ちきれるでしょうか?
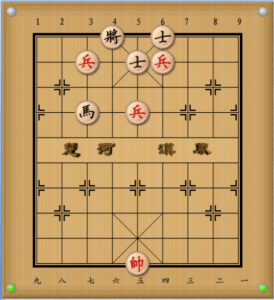
- 帥五進一 馬3退1
- 兵七平八 馬1進2
- 兵五進一 馬2退4
- 帥五平六 将4平5
- 帥六退一 馬4進6
- 兵五進一 士6進5
- 帥六平五 馬6退7
- 兵八平七 将5平4
- 帥五進一 士5退6(和)
実はこの「三兵対馬双士」の残局は、和の確率が非常に高い残局とされています。
勝つための考え方としては、1枚の兵を2枚の士と交換し「双兵対単馬」の勝てる形に持ち込むのが王道ですが、現実問題これはなかなか難しいです。
というのも、残局段階になり遮る駒が少なくなった馬はかなり自由に動けるので、それをかわしながら上手く攻めるのはかなり難易度が高くなります。
それではこの例題①についてより詳しく見ていきましょう!
まず2回合黒は馬1進2と上がりました。これは馬1進3だと再び兵取りになってしまい、兵八平七、馬3退1の繰り返しは黒の反則負けになってしまうからです。
ちなみに馬1進2ではなく、将4進1が気になった方もいるかもしれません。
この場合、兵五進一、士5退4、兵四進一、士4進5、兵四平五、士5進6、後兵平四、馬1進3、兵八平七、将4進1、帥五退1、馬3進5、兵四平三、馬5進4、兵三平四、馬4退5で和となります。
ただ途中一歩間違えたらすぐに紅勝ちになってしまうので、黒としては相当危なっかしい和の持ち込み方です
次に4回合紅が帥五退一とした場合を見てみましょう。
この場合黒は馬4進6と攻めを催促するのが正解で、以下兵五進一、士6進5、兵四平五、馬6退7、兵五平四、将4進1で和となります。
「双兵対単馬」の形にはなりましたが、この場合は馬6退7で兵をどかし将が上部脱出できるため、黒としてはなんとか和にすることができました。
ちなみに黒が間違って馬4進6ではなく将4進1とした場合、帥五平六で以下紅の勝ちになります。
また7回合黒が馬6退7の場面では、馬6退4でも和になります。
以下帥五進一、将5平4、帥五平六、将4平5、帥六平五、将5平4といった具合です。
最後に8回合、黒が将5平4ではなく馬7進5とした場合です。
一見これでも和になりそうですが、紅は構わず兵七平六とするのが好手。
以下馬5退4、兵四平五、将5平6(平4なら帥五平六で紅勝)、兵五平六と馬を取り、「単兵対弧将」で兵が2段目なので紅の必勝残局となります。
少し解説が長くなりましたが、なんとなく要領が掴めたでしょうか?
例題①は正しく指せば黒は和に持ち込める残局でしたが、間一髪といった感じで簡単ではありませんでしたね。
実戦では黒にミスが出る可能性が十分にあるので、紅を持った場合は一瞬のチャンスを逃さぬよう常にどうしたら勝てるかを意識しながら指すようにしましょう!
例題②
次はこの局面を見てみましょう!
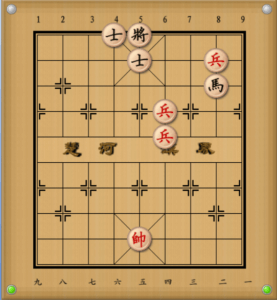
- 前兵進一 将5平6
- 前兵平三 馬8進9
- 兵二進一 馬9進7
- 兵三進一 将6平5
- 兵三平四 馬7進5
- 兵二平三 馬5退6
- 兵三平四 (紅勝)
「三兵対馬双士」は和の確率が高いものの必和残局ではないので、駒の位置関係次第では勝つこともできます。
紅はまず初手の前兵進一がポイントで、先に兵二平三などだと将5平6と出られて詰みません。
そして2回合前兵平三で馬をどかしたあとの兵二進一がポイントの一手です。
実はこの局面、兵三進一でも以下馬9退8、兵二進一、士5進4、兵二平三から「双兵対双士」に落とし込んで勝つことはできるのですが、一枚が底兵ですし手順がかなり長くなってしまいます。
兵二進一だと馬が引けないので、このほうがより分かりやすく簡潔です。
4回合紅の兵三進一は地味ながら着実な一手で、先に兵二平三だと将6進1で馬の守りがあるため詰みません。
そして最後、馬に一枚兵を取られますが、側面からの詰みがあるため紅の勝ちとなります。
それなりに難易度がある難しい局面だったと思いますが、この残局の時にはこういった勝ち方があるということだけでもしっかり覚えておきましょう!
まとめ
「三兵対馬双士」の残局は、
黒が正しく指せば和の確率がかなり高い。
ただ形次第では紅も勝てるので、必和残局ではない。
という結論になります。


